Tarefa 2º Bimestre

Olá alunos!

Esta é a nossa terceira tarefa. Vocês devem ler o texto e responder as questões que se encontram logo abaixo do mesmo. 

Leiam com muita atenção! As questões devem ser respondidas e enviadas para o e-mail: jeduardolante@gmail.com 

As perguntas referentes ao texto devem ser repondidas com suas próprias palavras, podendo conter citações de partes do texto. As respostas não podem ser cópias do texto. Vocês tem até o dia 15/06/2010 para enviar suas respostas, não deixem para última hora!

Vamos lá galera, muita disposição! Aguardo a participação de todos.

Abraços,

José Eduardo.

História dos Números Complexos

A história dos números complexos revela-se fascinante. Registros históricos mostram que, em 2500 AC, os Sumérios já tinham necessidade da subtração. Os números que conhecemos como inteiros negativos são resultados de certas subtrações. Por exemplo, em notação moderna, o resultado da subtração 5 – 10 é –5. Matemáticos não resistiram, ao longo da História,  à pressão da curiosidade de multiplicar números negativos dando origem ao conjunto numérico que atualmente denominamos de conjunto dos Números Inteiros: {0, ±1, ±2, ±3...}. Os Pitagóricos (550 AC) acreditavam que o mundo poderia ser compreendido por meio de razões da forma m/n (racionais) com m e n naturais e n distinto de zero. Contudo, esse modelo do mundo ruiu quando se descobriu que a medida da diagonal do quadrado, de lados medindo 1, é 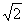. Ora,  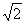não é razão de naturais! Além disso, os Pitagóricos descobriram muitos outros desse tipo: ,  , , , ... .
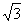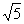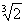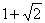Portanto, por necessidades intrínsecas da investigação matemática, o universo dos números naturais foi expandido amplamente. Durante o desenvolvimento da Álgebra, na Idade Média, os matemáticos italianos exploraram vários tipos de equações e classificaram suas soluções. Essa investigação mostrou que algumas equações não possuíam solução em termos dos números conhecidos. Um dos problemas enfrentados consistia na solução da equação x² + 1 = 0. Essa equação não parecia ter solução, pois contrariava o fato de que todo número real distinto de zero, quando elevado ao quadrado, é positivo. Os matemáticos indianos e árabes, quando se deparavam com essas equações se recusavam a definir algum símbolo para expressar a raiz quadrada de um número negativo, pois consideravam o problema completamente sem sentido. No Século XVI, raízes quadradas de números negativos começaram a aparecer em textos algébricos, porém os autores frisavam que as expressões não possuíam significado e utilizavam termos tais como ”fictícias”, “impossíveis”, “sofisticadas”, para mencioná-las. O matemático alemão Leibniz (1646-1716), um dos inventores do Cálculo Diferencial, atribuía à raiz quadrada de –1 um certo caráter metafísico interpretando-a como uma manifestação do “Espírito Divino”; a mesma sensação de espanto sucedeu com o matemático suíço Lenhard Euler.

Alguns matemáticos europeus, em particular os italianos Gerolamo Cardano e Rafaello Bombelli, introduziram os números complexos na Álgebra, durante o Século XVI, quando eles assumiram a existência de raízes quadradas de números negativos, apesar de considerarem tais raízes “números impossíveis” e, assim, denominá-los “números imaginários”. Por esse motivo, até hoje perdura o nome de números imaginários quando nos referimos a raízes quadradas de números negativos. Postulando a existência de raízes quadradas de inteiros negativos, e assumindo que i é solução da equação x² + 1 = 0, ou seja, axiomatizando–se que i satisfaz a relação i² = –1, pode-se efetuar operações envolvendo i e os números reais. Dessa forma, para qualquer número real positivo a, a raiz quadrada do número negativo –a é i 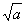, ou seja,  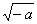 =  i .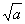

Dados os números reais c e d, podemos multiplicar d por i e obter i d, e adicionar a c para obtermos c + i d. Em geral, qualquer número complexo é escrito como c + d i, onde c é denominado “parte real” e d “parte imaginária”.  Portanto, obtemos números da forma c + i d formando o conjunto dos números complexos. No conjunto dos números complexos, podemos adicionar e multiplicar formando uma estrutura algébrica denominada corpo dos números complexos.

Os matemáticos costumam representar os números reais como pontos em uma reta denominada de reta real, onde a cada ponto corresponde um único número real e a cada número real associam um único ponto dessa reta. Como a raiz quadrada de um número negativo não pode ser representada nessa reta, persistiu um impasse até o Século XIX. O primeiro a propor uma visualização dos complexos identificando-os como pontos do plano bidimensional foi o autodidata norueguês Caspar Wessel em 1797. Essa idéia foi redescoberta por Jean-Robert Argand, um contador suíço, que publicou um livro em 1860 sobre o assunto, e também pelo genial matemático alemão Karl Friedrich Gauss. Como era impossível associar um ponto da reta real à raiz quadrada de um número negativo, a questão foi resolvida associando-se aos números imaginários pontos sobre uma reta perpendicular à reta real, passando pelo ponto zero, e dessa forma criando um sistema de coordenadas cartesianas. Nesse sistema, os números reais são colocados sobre o eixo horizontal, denominado eixo real, e todos os números imaginários sobre a reta perpendicular à reta real, passando pelo zero da reta real horizontal, denominado de eixo imaginário. 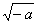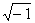Como  =   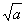= i 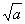, todos os números  imaginários podem ser colocados no eixo imaginário como múltiplos de i = .

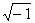Portanto, não só os imaginários passam a ter uma representação gráfica, como as combinações possíveis de reais e imaginários, ou seja, os números complexos, são representados por pontos no plano definido pelos eixos real e imaginário, denominado plano complexo.

O talento e a genialidade de Gauss levaram a um dos resultados mais profundos da Matemática, o Teorema Fundamenta Álgebra, que afirma que toda equação polinomial possui solução no corpo dos números complexos. Além desse resultado importantíssimo, a álgebra dos números complexos originou uma nova área de investigação — a Análise Complexa — que tem um papel fundamental no desenvolvimento da Álgebra e da Teoria dos Números. Os números complexos representam uma das estruturas mais importantes da Ciência. Atualmente, é impossível imaginar a Engenharia Elétrica, a Aerodinâmica, ou a Dinâmica dos Fluidos, sem os números complexos. A Mecânica Quântica faz uso dos números complexos e, na Teoria da Relatividade de Einstein, o espaço tridimensional é visto como real e a dimensão relativa ao tempo como imaginário. 

Números Complexos, uma abordagem histórica 

A questão central desta página é "Como surgiram os Números Complexos?".

A maioria das pessoas, quando confrontadas com esta questão respondem que surgiram para resolver as equações de 2º grau da forma  x² + a = 0, sendo a um número positivo. No entanto, esta ideia está errada!

A abordagem aprofundada aos números complexos, apesar de ter sido feita a partir do séc. XVIII, foi mencionada levemente por outros matemáticos anteriores à data. No entanto, dada a incompreensão e o desconhecimento destes números, tais matemáticos abandonaram o seu estudo.

O primeiro matemático de que se tem conhecimento de se ter deparado com um problema que envolvia números complexos foi Héron de Alexandria (séc. I dC) no livro Stereometrica. Este pretendia resolver a expressão:

Mas como não havia o domínio atual sobre estes números, abandonou o seu cálculo.

Por volta do ano 275 dC, Diophanto (200-284 aprox.) ao resolver um problema deparou-se com a equação 24x² - 172x + 336 = 0. Como concluiu que não tinha soluções reais, não viu necessidade de dar sentido à raiz  

 Bhaskara (1114-1185 aprox.), um dos indianos que mais perto chegou das ideias da álgebra moderna (conhecia a regra "menos por menos dá mais", trabalhava com coeficientes negativos, etc.) reconhecia que a equação  x² - 45x = 250 era satisfeita por dois valores x = 5 e x = -5 mas, dizia que não considerava a segunda pois as pessoas não "apreciavam" raízes negativas.

Gerônimo Cardano (1501-1576) considerava que o aparecimento de raízes quadradas de números negativos na resolução de um problema indicava que o mesmo não tinha solução. No entanto, foi Cardano que, em 1545, mencionou pela primeira vez os números complexos. Na sua obra Ars Magna de Cardano, falava do seguinte problema: "Determinar dois números cuja soma seja 10 e o produto seja 40". Para tal, considerou as expressões:

Cardano ficou por aqui, não dando significado a estas expressões, pondo de lado a "tortura mental" envolvida, mas teve o mérito de ter sido o primeiro a considerá-las, até porque neste tempo os números negativos eram evitados.

A partir disto é possível derrubar a ideia errada de que os números complexos surgiram com as equações do segundo grau. Os números complexos apareceram sim, a partir das equações de terceiro grau.

Mas, foram preciso cerca de 25 anos para este tema ser de novo considerado, por  Raffaelle Bombelli (1526-1572) numa obra de nome Algebra.

Ao resolver a equação x³ = 15x + 4, Bombelli utilizou a "fórmula de Cardano" obtendo a seguinte solução (em notação moderna):

Ele achou estranho este resultado porque conhecia todas as raízes da equação, entre as quais  x = 4. Teve então a estranha ideia de procurar a e b positivos tais que:

Com alguma manipulação algébrica, usando as mesmas regras que usava para os números reais, mais a propriedade,

chegou ao resultado a = 2 e b = 1, donde sai x = 4.

O próprio Bombelli não estava bem seguro do que havia criado. Para os demais matemáticos da época, os números complexos eram vistos com suspeita e quanto muito tolerados, na falta de melhor coisa.

É de referir que alguns matemáticos da época procuraram maneiras de evitar o uso de tais números. Entre eles, Cardano foi o que mais tentou evitar as "torturas mentais" envolvidas no uso de raízes quadradas de negativos. No seu livro De Regula Aliza, de 1570, procurou artifícios que contornassem o uso de tais raízes na resolução de equações de 3º grau obtendo, somente, resultados vagos. 

Raffaelle Bombelli apresentou na sua obra Algebra as leis algébricas que regiam os cálculos entre números da forma :

Em particular, mostrou que as 4 operações aritméticas sobre números complexos produzem números desta forma. Ou seja, o conjunto dos complexos é fechado para estas operações.

Em 1629, Albert Girard (1595-1632) utiliza, efectivamente, o símbolo Ö-1 quando enuncia as relações entre raízes e coeficientes de uma equação.

Um grande passo no estudo dos números complexos foi a sua representação visual. Em 1797, o dinamarquês Caspar Wessel (1745-1818) representou, pela primeira vez, geometricamente os números complexos, estabelecendo uma correspondência bijectiva entre estes e os pontos do plano.
Este trabalho foi levado ao esquecimento, talvez por ter sido publicado em dinamarquês e só por volta de 1806, quando publicado em francês por Jean Argand (1768-1822) ganhou o devido respeito. Por este motivo, esta representação ficou, indevidamente, ligada ao nome de Argand.

É pois possível dizer que, apesar da sua história ser recente, os números complexos envolveram o trabalho de vários matemáticos continuando, ainda  hoje, muitas questões em aberto.

ão 5